Atoms of a Solid Line Up in a Repeats Over and Over Again
Properties of Solids
Equally y'all should think from the kinetic molecular theory, the molecules in solids are non moving in the same mode every bit those in liquids or gases. Solid molecules simply vibrate and rotate in identify rather than movement nearly. Solids are generally held together by ionic or strong covalent bonding, and the attractive forces betwixt the atoms, ions, or molecules in solids are very strong. In fact, these forces are so strong that particles in a solid are held in fixed positions and have very little liberty of movement. Solids have definite shapes and definite volumes and are non compressible to any extent.
At that place are 2 main categories of solids—crystalline solids and baggy solids. Crystalline solids are those in which the atoms, ions, or molecules that make upwardly the solid exist in a regular, well-defined system. The smallest repeating pattern of crystalline solids is known as the unit cell, and unit cells are like bricks in a wall—they are all identical and repeating. The other chief blazon of solids are called the amorphous solids. Baggy solids do not have much order in their structures. Though their molecules are close together and have lilliputian freedom to move, they are not arranged in a regular order as are those in crystalline solids. Common examples of this type of solid are drinking glass and plastics.
There are four types of crystalline solids:
Ionic solids—Fabricated up of positive and negative ions and held together by electrostatic attractions. They're characterized by very high melting points and brittleness and are poor conductors in the solid state. An instance of an ionic solid is table table salt, NaCl.
Molecular solids—Made up of atoms or molecules held together by London dispersion forces, dipole-dipole forces, or hydrogen bonds. Characterized by depression melting points and flexibility and are poor conductors. An example of a molecular solid is sucrose.
Covalent-network (also called diminutive) solids—Made up of atoms connected past covalent bonds; the intermolecular forces are covalent bonds as well. Characterized equally being very hard with very loftier melting points and being poor conductors. Examples of this type of solid are diamond and graphite, and the fullerenes. As you lot can encounter below, graphite has only 2-D hexagonal structure and therefore is non hard like diamond. The sheets of graphite are held together by only weak London forces!
Metallic solids—Made up of metal atoms that are held together by metal bonds. Characterized past high melting points, can range from soft and malleable to very difficult, and are good conductors of electricity.
CRYSTAL STRUCTURES WITH CUBIC UNIT CELLS (From https://eee.uci.edu/programs/gchem/RDGcrystalstruct.pdf)
Crystalline solids are a three dimensional collection of private atoms, ions, or whole molecules organized in repeating patterns. These atoms, ions, or molecules are called lattice points and are typically visualized equally round spheres. The two dimensional layers of a solid are created past packing the lattice point "spheres" into square or closed packed arrays. (Run across Below).
Figure one: Two possible arrangements for identical atoms in a two-D structure
Stacking the two dimensional layers on top of each other creates a three dimensional lattice point system represented by a unit prison cell. A unit cell is the smallest collectionof lattice points that can exist repeated to create the crystalline solid. The solid tin exist envisioned every bit the consequence of the stacking a great number of unit cells together. The unit cell of a solid is determined past the blazon of layer (square or close packed), the fashion each successive layer is placed on the layer beneath, and the coordination number for each lattice signal (the number of "spheres" touching the "sphere" of involvement.)
Primitive (Simple) Cubic Structure
Placing a second square assortment layer straight over a first square array layer forms a "simple cubic" construction. The simple "cube" advent of the resulting unit of measurement jail cell (Figure 3a) is the basis for the name of this three dimensional structure. This packing system is often symbolized as "AA...", the letters refer to the repeating social club of the layers, starting with the lesser layer. The coordination number of each lattice point is six. This becomes apparent when inspecting role of an next unit cell (Figure 3b). The unit jail cell in Figure 3a appears to comprise viii corner spheres, however, the total number of spheres inside the unit cell is 1 (only i/8th of each sphere is actually inside the unit prison cell). The remaining seven/8ths of each corner sphere resides in seven adjacent unit cells.
The considerable space shown betwixt the spheres in Figures 3b is misleading: lattice points in solids touch as shown in Figure 3c. For example, the distance betwixt the centers of two adjacent metallic atoms is equal to the sum of their radii. Refer once more to Effigy 3b and imagine the adjacent atoms are touching. The edge of the unit cell is and then equal to 2r (where r = radius of the atom or ion) and the value of the face diagonal equally a function of r tin be establish by applying Pythagorean's theorem (a2 + btwo = c2) to the right triangle created past two edges and a face diagonal (Effigy 4a). Reapplication of the theorem to another right triangle created by an edge, a confront diagonal, and the torso diagonal allows for the determination of the body diagonal as a function of r (Figure 4b).
Few metals prefer the simple cubic construction because of inefficient apply of space. The density of a crystalline solid is related to its "percentage packing efficiency". The packing efficiency of a elementary cubic structure is only about 52%. (48% is empty space!)
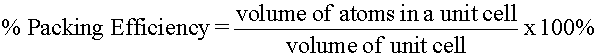
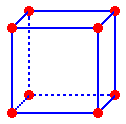
Body Centered Cubic (bcc) Construction
A more efficiently packed cubic structure is the "body-centered cubic" (bcc). The first layer of a square array is expanded slightly in all directions. Then, the second layer is shifted so its spheres nestle in the spaces of the first layer (Figures 5a, b). This repeating club of the layers is frequently symbolized as "ABA...". Similar Figure 3b, the considerable space shown between the spheres in Effigy 5b is misleading: spheres are closely packed in bcc solids and impact along the body diagonal. The packing efficiency of the bcc structure is about 68%. The coordination number for an atom in the bcc structure is eight. How many total atoms are at that place in the unit cell for a bcc structure? Draw a diagonal line connecting the three atoms marked with an "10" in Figure 5b. Assuming the atoms marked "x" are the aforementioned size, tightly packed and touching, what is the value of this torso diagonal every bit a role of r, the radius? Notice the edge and volume of the cell as a part of r.
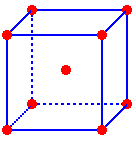
Cubic Closest Packed (ccp)
A cubic closest packed (ccp) structure is created by layering close packed arrays. The spheres of the second layer nestle in half of the spaces of the first layer. The spheres of the 3rd layer directly overlay the other half of the first layer spaces while nestling in half the spaces of the second layer. The repeating society of the layers is "ABC..." (Figures 6 & 7). The coordination number of an atom in the ccp construction is twelve (six nearest neighbors plus three atoms in layers to a higher place and beneath) and the packing efficiency is 74%.
Figure 6: Shut packed Array Layering. The 1st and 3rd layers are represented by light
spheres; the 2d layer, dark spheres. The 2d layer spheres nestle in the spaces of the 1st
layer marked with an "x". The 3rd layer spheres nestle in the spaces of the 2nd layer that
directly overlay the spaces marked with a "·" in the 1st layer.
Figure 7a & 7b: Ii views of the Cubic Close Packed Construction
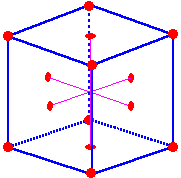
If the cubic close packed construction is rotated past 45° the face centered cube (fcc) unit cell can be viewed (Figure 8). The fcc unit prison cell contains viii corner atoms and an atom in each face up. The face atoms are shared with an adjacent unit prison cell so each unit of measurement cell contains ½ a face atom. Atoms of the face centered cubic (fcc) unit cell bear upon across the face diagonal (Figure 9). What is the border, confront diagonal, body diagonal, and book of a confront centered cubic unit cell as a part of the radius?
Effigy 8: The face centered cubic unit of measurement prison cell is drawn by cutting a diagonal plane through
an ABCA packing arrangement of the ccp structure. The unit jail cell has four atoms (one/8 of
each corner atom and ½ of each confront atom).
Figure 9a:Space filling model of fcc. Figure 9b: The face of fcc. Confront diagonal = 4r.
Ionic Solids
In ionic compounds, the larger ions become the lattice betoken "spheres" that are the framework of the unit of measurement cell. The smaller ions nestle into the depressions (the "holes") between the larger ions. In that location are three types of holes: "cubic", "octahedral", and "tetrahedral". Cubic and octahedral holes occur in foursquare assortment structures; tetrahedral and octahedral holes announced in shut-packed array structures (Figure 10). Which is usually the larger ion – the cation or the anion? How can the periodic table be used to predict ion size? What is the coordination number of an ion in a tetrahedral pigsty? an octahedral hole? a cubic hole?
Figure 10. Holes in ionic crystals are more like "dimples" or "depressions" between the
closely packed ions. Small ions can fit into these holes and are surrounded by larger ions
of opposite charge.
The blazon of pigsty formed in an ionic solid largely depends on the ratio of the smaller ion'due south radius the larger ion'southward radius (rsmaller/rlarger). (Table 1).
Empirical Formula of an Ionic Solid
Two ways to determine the empirical formula of an ionic solid are: 1) from the number of each ion contained within i unit cell 2) from the ratio of the coordination numbers of the cations and anions in the solid.
Example: Find the empirical formula for the ionic chemical compound shown in Figures 11 & 12.First Method: When using the first method, remember near atoms in a unit cell are shared with other cells. Table 2 lists types of atoms and the fraction contained in the unit cell. The number of each ion in the unit prison cell is determined: one/8 of each of the 8 corner X ions and i/4 of each of the 12 border Y ions are institute within a single unit jail cell. Therefore, the cell contains ane 10 ion (8/8 = 1) for every iii Y ions (12/4 = three) giving an empirical formula of XY3. Which is the cation? anion? When writing the formula of ionic solids, which comes start?
Second Method: The 2nd method is less reliable and requires the examination of the crystal structure to decide the number of cations surrounding an anion and vice versa. The structure must be expanded to include more than unit of measurement cells. Figure 12 shows the same solid in Effigy xi expanded to 4 adjacent unit cells. Test of the construction shows that in that location are 2 X ions coordinated to every Y ion and 6 Y ions surrounding every Ten ion. (An additional unit cell must be projected in forepart of the page to see the sixth Y ion ). A 2 to 6 ratio gives the same empirical formula, XY3.
Summary:
| Unproblematic Cubic: 1 full atom per cell (1/8 each corner) | Torso Centered Cubic: two atoms per cell (i in center and ane/8 for each corner) | Face Centered Cubic: 4 atoms per prison cell |
|---|
Source: https://www.chem.fsu.edu/chemlab/chm1046course/solids.html
0 Response to "Atoms of a Solid Line Up in a Repeats Over and Over Again"
Post a Comment